K-Nearest Neighbors

Posted on | In

[ML] KNN 기본 개념 및 장단점

Week#5-1 / Video / Reference: Prof.Choi

K-Nearest Neighbors

K-최근접 이웃

KNN은 지도학습의 대표적 machine learning 방법이다. 크게 다음과 같이 두 가지로 나눌 수 있다.

  • Classification 분류

    얼굴 인식, 숫자 판별 (MNIST) 등

    미리 정의된, 가능성 있는 여러 class label 중 하나를 예측하는 것이다.

    • Binary Classification: 두 개의 class로만 나눔
    • Multiclass Classification: 셋 이상의 class로 나눔

  • Regression 회귀

    주식 가격을 예측하여 수익을 내는 알고리즘 등

    연속적인 숫자 또는 부동소수점수(실수)를 예측하는 것이다.

이번 포스팅에서는 먼저 KNN classification에 대해 다뤄볼 예정이다. 본격적으로 들어가기에 앞서 KNN의 개념부터 살펴보자.

Concept

knn

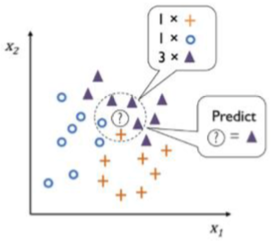
KNN이란 주변 k개 자료의 class 중 가장 많은 class로 특정 자료를 분류하는 방식이다. 쉽게 말하자면 새로운 자료 ? 를 가장 가까운 n개의 자료 (k=n)를 이용, 투표하여 가장 많은 class로 할당하는 것이라 볼 수 있다. 이때 training data 자체가 모형일 뿐, 어떠한 추정 방법도 모형도 없다. 즉, 데이터 분포를 표현하기 위한 파라미터를 추정하지 않는다. 매우 간단한 방법임에도 불구하고 performance는 떨어지지 않는다.

Lazy learner 게으른 학습, Instance-based learning 사례 중심 학습이라고도 불린다. 이는 Model-based learning과 반대되는 개념이다. 훈련 data에서 discriminative function을 학습하는 대신, 훈련 dataset을 memory에 저장하는 방법을 사용한다. 하지만 KNN은 차원이 증가할수록 성능 저하가 심하다는 단점이 있다. Curse of dimension 이라고도 부른다. 데이터의 차원이 증가할수록 해당 공간의 크기(부피)가 기하급수적으로 증가하여 동일한 개수 데이터의 밀도가 급속도로 희박(Sparce)해지기 때문이다.

차원의 저주 차원이 증가할수록 데이터의 분포 분석에 필요한 sample data의 개수가 기하급수적으로 증가하는 어려움을 표현한 용어

KNN은 𝑖번째 관측치와 𝑗번째 관측치의 거리로 Minkowski distance를 이용한다.

실제 parameter 값으로는 p=1 맨하탄 거리, p=2 유클리디언 거리를 사용한다.

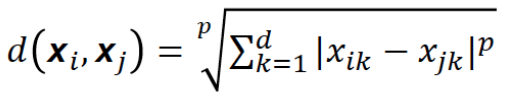
minkowski

Hyper-parameters

  • 탐색할 이웃 수(k)와 거리 측정 방법

    • Overfitting: k가 작을 경우 데이터의 지역적 특성을 지나치게 반영하여 과적합이 발생한다. 1-NN의 경우 데이터 경향성을 파악하지 못하므로 새로운 데이터가 들어왔을 때 오판을 내릴 가능성이 크다.
    • Underfitting: 반대로 k가 매우 클 경우 모델이 과하게 정규화된다.

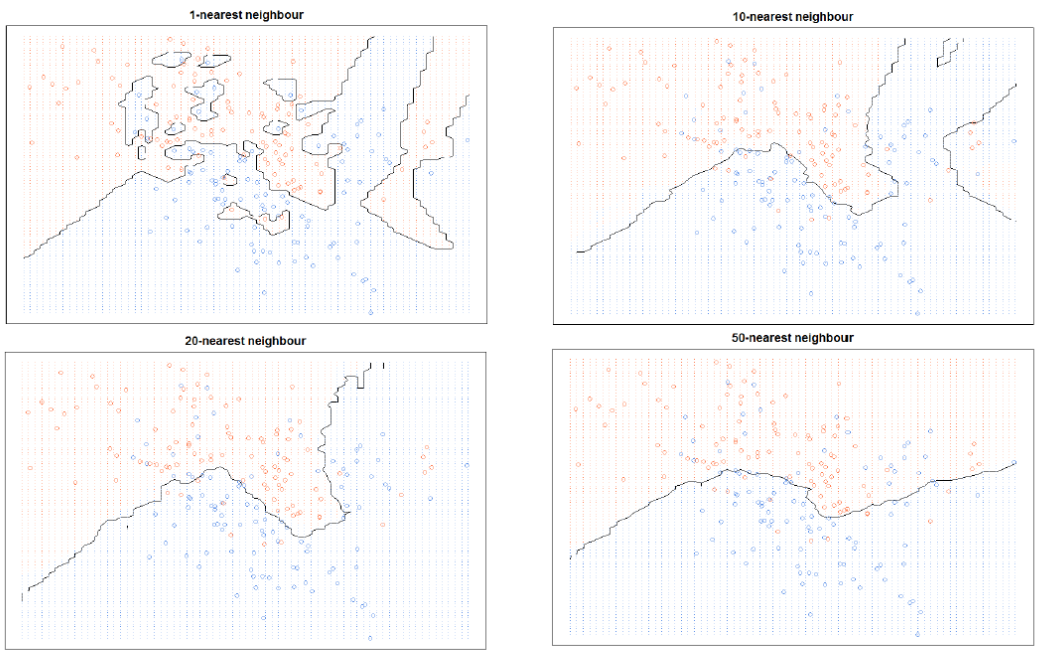
    over-under

    위의 두 방식 모두 좋은 학습 결과가 아니다. Distance metric은 실험적으로 선택하여 적절히 사용해야 한다.

  • Voting 방식

    • Majority voting: 다수결 방식이다. 이웃 범주들 중 빈도가 제일 많은 범주로 새 데이터의 범주를 예측한다.
    • Weighted voting: 가중 합 방식이다. 가까운 이웃의 정보에 좀 더 가중치를 부여하여 예측한다.

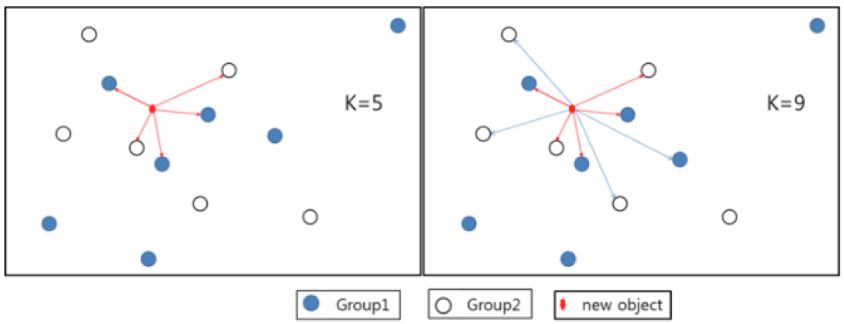
    voting

    New object에 대해 근접치 k의 개수에 따라 group이 달리 분류되는 것을 확인할 수 있다. 위 그림에서는 다수결 방식을 사용했을 때는 k값이 바뀌면 new object의 class가 변경되지만 가중 합 방식을 사용하면 class가 변하지 않는다.

Pros and Cons

  • 장점

    • 학습 데이터 내에 끼어있는 noise의 영향을 크게 받지 않음

    • 학습 데이터 수가 많다면 꽤 효과적인 알고리즘

    • Mahalanobis 거리와 같이 데이터의 분산을 고려할 경우 매우 robust한 방법론

      Mahalanobis distance 평균과의 거리가 표준편차의 몇 배인지를 나타내는 값이다. 즉, 어떤 값이 얼마나 일어나기 힘든 값인지, 또는 얼마나 이상한 값인지를 수치화하는 한 방법이다.

  • 단점

    • 최적 이웃 수(k)와 distance metric이 분석에 적합한지 불분명하므로 데이터 각각의 특성에 맞게 연구자가 임의로 선정해야 함. 한마디로 귀찮음.

      Best k 는 데이터마다 다르기 때문에 Grid Search로 탐색할 수 있다. 이와 관련해서는 추후 공부할 예정이다.

    • 새로운 관측치와 각각의 학습 데이터 사이 거리를 전부 측정해야 하므로 계산 시간이 오래 걸리는 한계 존재

      Locality Sensitive Hashing(LSH), Network based Indexer, Optimized product quantization 등은 KNN의 계산 복잡성을 줄이려는 시도들이다.