Multiple Linear Regression

Posted on | In

[ML] 다중 선형 회귀와 정규화

Week#6-1 / Video / Reference: Prof.Choi

Multiple Linear Regression

다중 선형 회귀란 수치형 설명변수 X, 연속형 숫자로 이루어진 종속변수 Y(범주형 아님) 간의 관계를 선형으로 가정하고 이를 가장 잘 표현할 수 있는 회귀계수를 데이터로부터 추정하는 모델이다.

y = f(x)

에서 f 함수가 결국 X와 Y의 관계가 되는 것이며, 이것을 선형으로 가정한다. 만약 n개의 데이터, k개의 설명변수(𝑥11, …, 𝑥nk), k개의 회귀 계수(β0, …, βk)가 있다고 하면 다중선형회귀 모델 방정식은 다음과 같다.

1

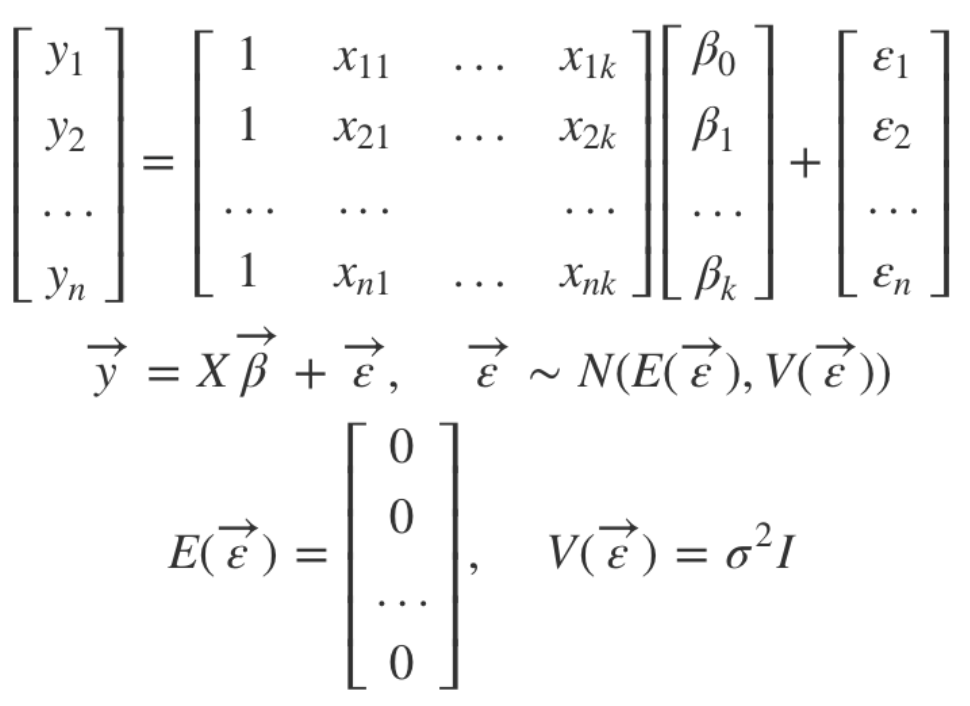
Y = β0 + β1𝑥1 + β2𝑥2 + … + βk𝑥k

위에서 β0 ~ βk까지가 우리가 추정하여 찾아야 하는 회귀 변수가 된다.

회귀 계수 결정법

회귀 계수를 결정하기 위해서는 다음과 같은 방법을 이용한다.

  • Direct Solution

    • 선형 회귀의 계수들은 실제값(Y)와 모델 예측값(Y’)의 차이, 오차제곱합(error sum of squares)을 최소로 하는 값으로 선정한다.

    • 최적의 계수들은 회귀 계수에 대해 미분한 식을 0으로 놓고 풀면 명시적인 해를 구할 수 있다. 즉, X와 Y 데이터만으로 회귀 계수를 구할 수 있는 것이다.

      이차함수 그래프의 꼭지점 같은 느낌이다.

    2

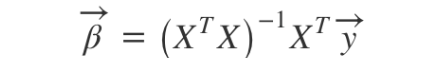
  • Numerical Search

    대표적으로 Gradient Descent(경사하강법)을 사용한다. 경사하강법이란 어떤 함수 값(목적 함수, 비용 함수, 에러 값)을 최소화하기 위해 임의의 시작점을 잡은 후 해당 지점에서의 gradient(경사)를 구하고, 그 반대 방향으로 조금씩 이동하는 과정을 반복하는 것이다. 더 이상 움직일 필요가 없을 때까지.

    Learning rate gradient의 이동 정도이다. 너무 크게 잡으면 발산해버린다.

    • Batch Gradient Descent (GD) 지드래곤 아님 이찬혁 아님

      • parameter를 update할 때마다 모든 학습 데이터를 사용하여 cost function의 gradient를 계산한다.

      • Vanilla Gradient Descent, Full Batch 라고도 한다.

        보통 바닐라 아이스크림이 기본 맛이라서 그렇다고 한다

      • 학습 효율이 매우 낮다.

    • Stochastic Gradient Descent (SGD)

      • 무작위로 sampling된 학습 데이터를 하나씩만 이용하여 cost function의 gradient를 계산한다.
      • 모델을 자주 update하며, 성능 개선 정도를 빠르게 확인할 수 있다.
      • logical minina에 빠질 가능성을 줄일 수 있으나, 최소 cost에 수렴했는지의 판단이 상대적으로 어렵다.

    • Mini Batch Gradient Descent

      • 일정량의 일부 데이터를 무작위로 뽑아 cost function의 gradient를 계산한다.
      • GD와 SGD를 혼합한 개념이다. SGD의 noise를 줄이면서, GD의 전체 배치보다 효율적이기 때문에 널리 사용되는 기법이다.

    3

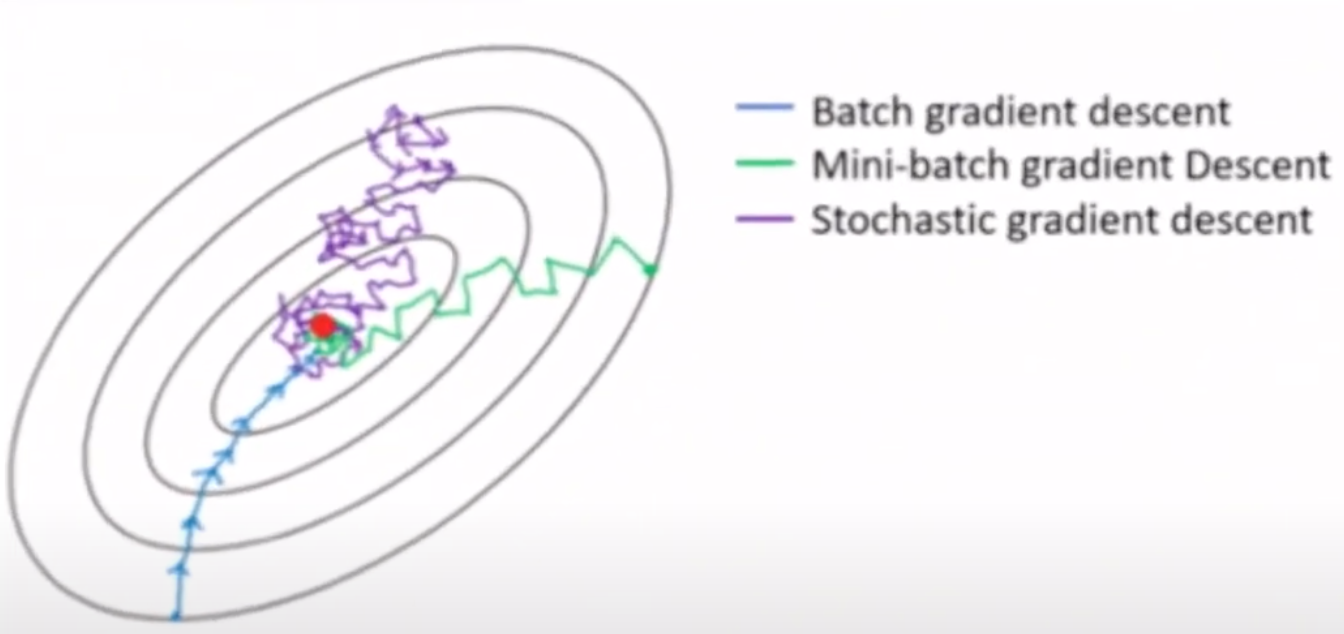
    3차원 그래프를 등고선처럼 표현한 그림이다. 이외 다른 방법론들에 관심이 있다면 pytorch, scikit-learn 등에서 solver option을 찾아보자. 그곳에 링크된 논문 등을 참고하면 된다.

Regularization

정규화란 회귀 계수가 가질 수 있는 값에 제약 조건을 부여하여 미래 데이터에 대한 오차를 기대한다. 이 기대 값은 모델의 Bias와 variance로 분해할 수 있는데, 정규화는 variance를 감소시켜 일반화 성능을 높이는 기법이다.

단, 이 과정에서 bias가 증가할 수 있다.

4

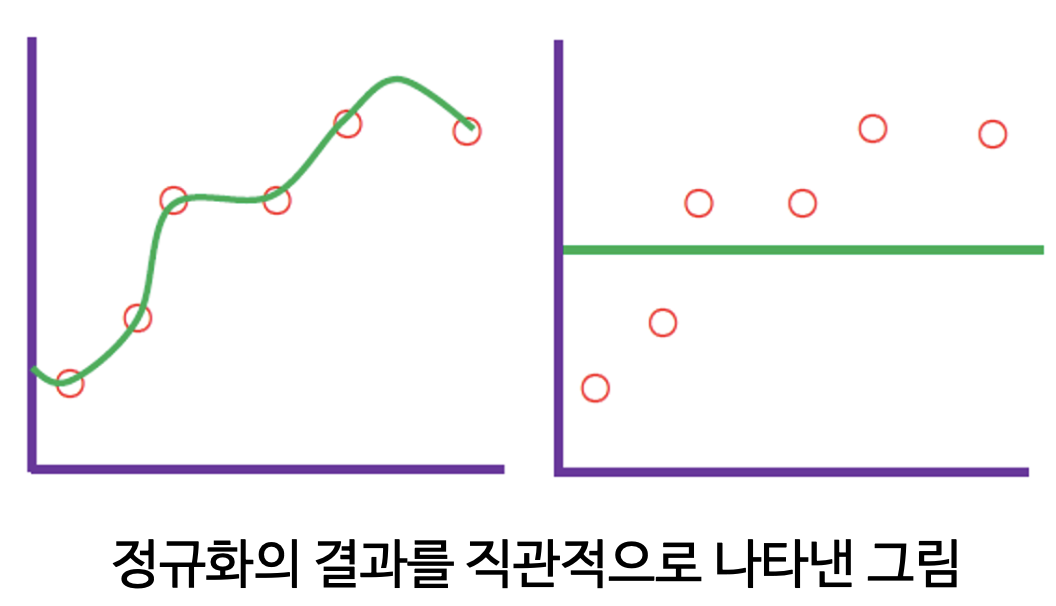
왼쪽 그림은 학습 데이터를 정말 잘 맞추고 있지만, 미래 데이터가 조금만 바뀌어도 예측 값이 들쭉날쭉할 수 있다. 오른쪽 그림은 가장 강한 수준의 정규화를 수행한 결과로, 학습 데이터에 대한 설명력을 다소 포기하는 대신 미래 데이터 변화에 상대적으로 안정적인 결과를 나타낸다.

  • Bias-Variance Decomposition

    Generalization(일반화, 정규화의 확장 개념) 성능을 높이는 정규화, ensemble 기법의 이론적 배경이다. 학습에 쓰지 않은 미래 데이터에 대한 오차의 기대 값을 모델의 bias와 variance로 분해하자는 내용이다.

    best는 둘 다 작은 거다.

    5

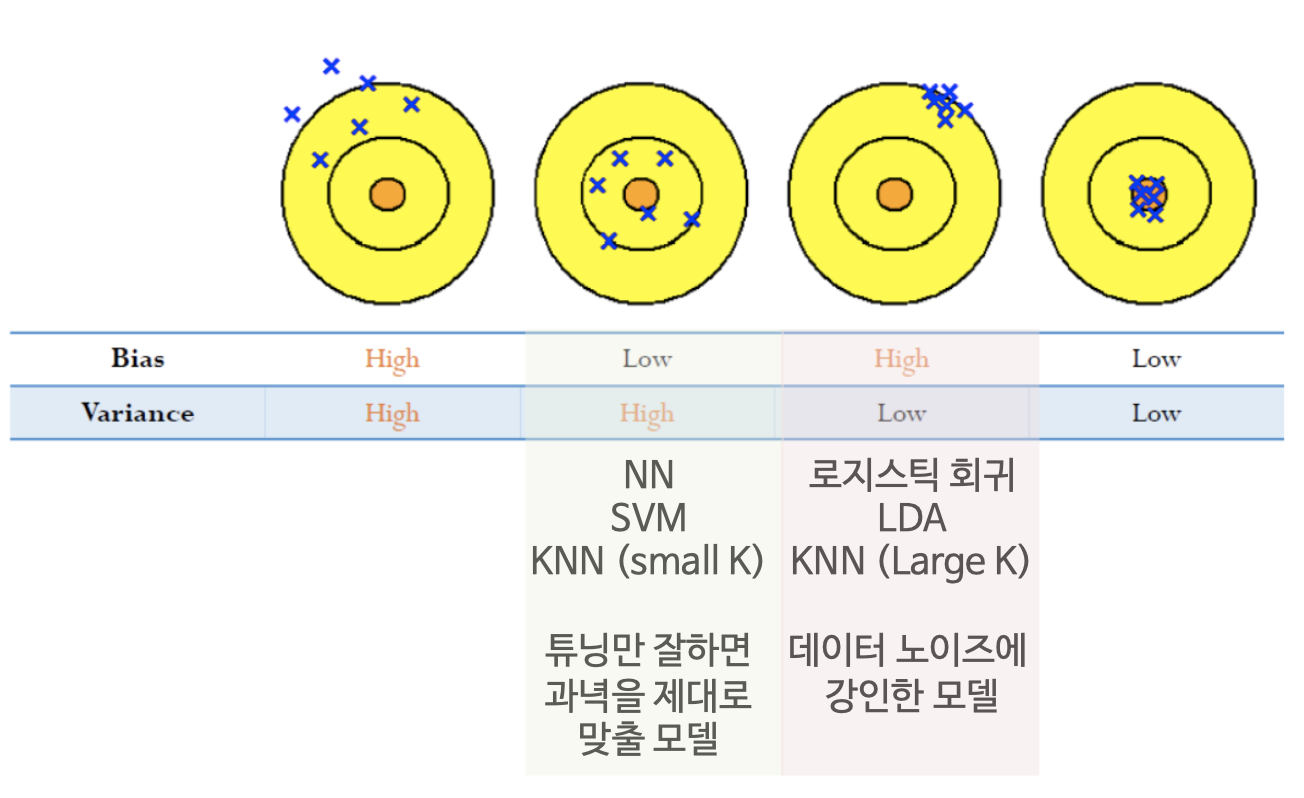
    과녁에 총을 쏜다고 하자. Bias 조정은 클리크 조정, Variance는 탄착군이라고 보면 된다. 군필들은 이해가 쉬울 것이다. 밀집된 탄착군을 형성할 만큼 실력이 좋아도 클리크가 어긋나면 세 번째 과녁과 같은 상황이 벌어질 것이고, 클리크가 완벽해도 실력이 좋지 않으면 두 번째 과녁처럼 엉성한 탄착군을 확인할 수 있을 것이다.

    4-1

    군 시절 쐈다 하면 만발이었다 M4A1 Carbin / ACOG(4배율 스코프) / 수직 손잡이 덕분

    우리는 Boosting 기법을 이용해 bias를 줄이고, Lasso Regression 기법을 이용해 variance를 줄일 수 있다.