[ML] 로지스틱 회귀
Week#6-2 / Video / Reference: Prof.Choi
앞서 공부한 Multiple Linear Regression의 예시를 두 가지 들어보겠다.
-
33명의 성인 여성에 대한 나이와 혈압 데이터
-
오차제곱합을 최소로 하는 회귀 계수 계산 결과 및 분석:
SBP = 81.54 + 1.222AGE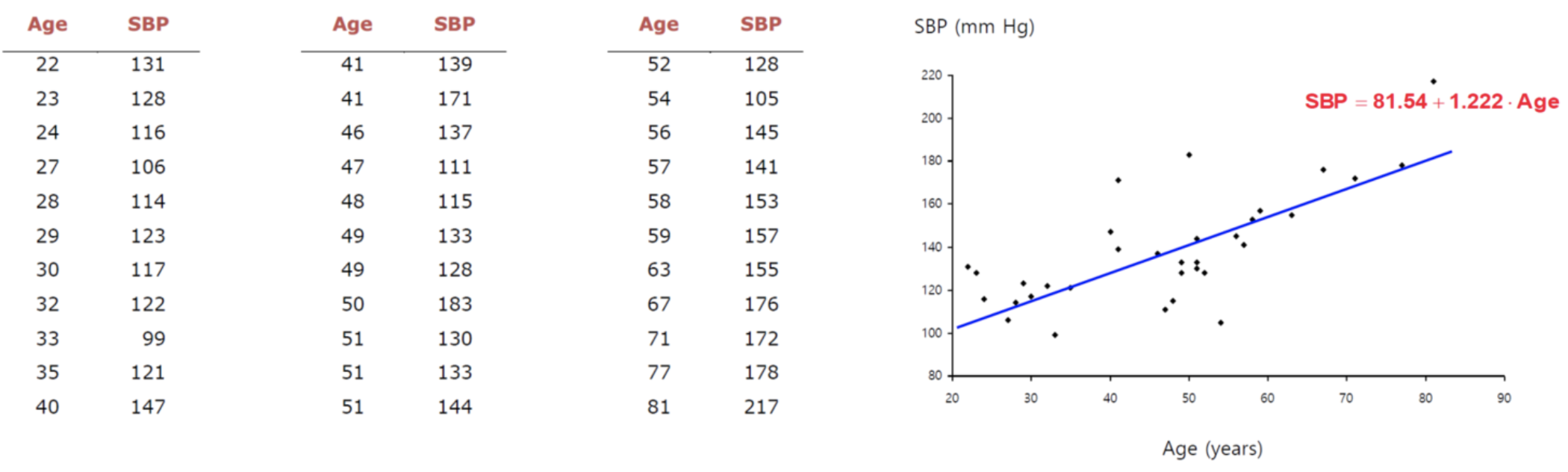
나이라는 변수에 대응하는 계수는 1.222로 나타났는데, 이는 나이를 한 살 더 먹으면 혈압이 1.222mm/Hg만큼 증가한다는 결과를 보여준다. Linear Regression 사용 가능
-
-
33명의 성인 여성에 대한 나이(Age)와 암 발병(CD) 데이터
-
오차제곱합을 최소로 하는 회귀 계수 계산 결과 및 분석:

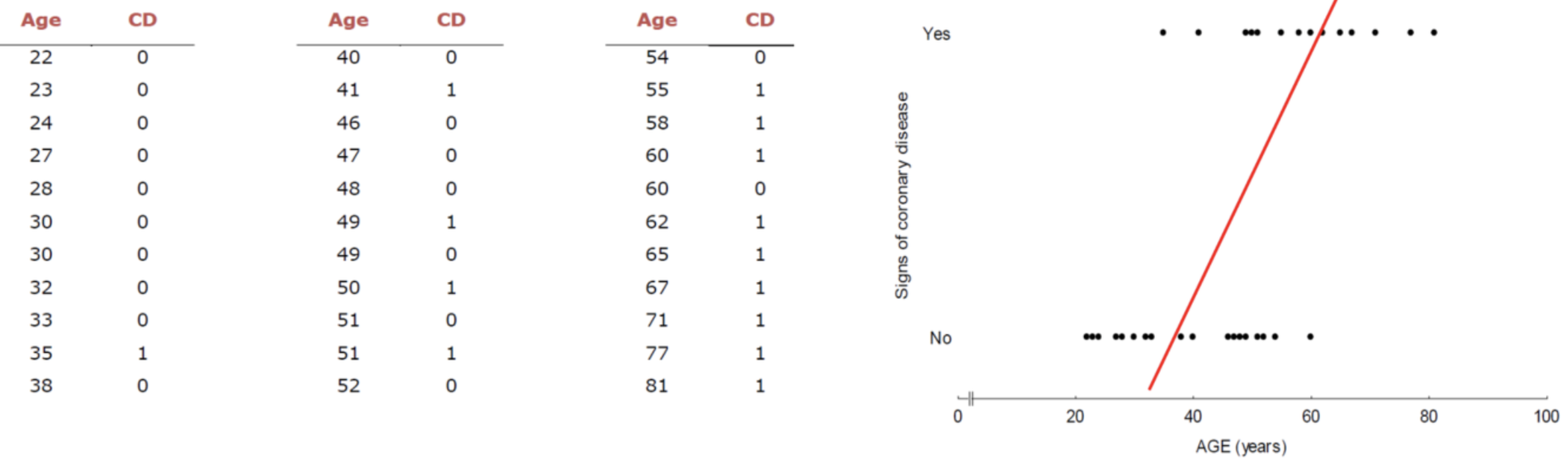
범주형 숫자(암 발병 여부)는 연속형 숫자(혈압)과 달리 의미를 지니지 않는다. 즉, 0(정상)과 1(발병)을 서로 바꾸어도 상관이 없다. Linear Regression 사용 불가
-
두 번째 예시와 같이 범주형 숫자의 경우는 Logistic Regression, 로지스틱 회귀 모델을 적용할 수 있다. 이 방향성, 선형 회귀에서 선형 분류로 넘어가는 방향성을 기억하는 것이 중요하다.
Logistic Function
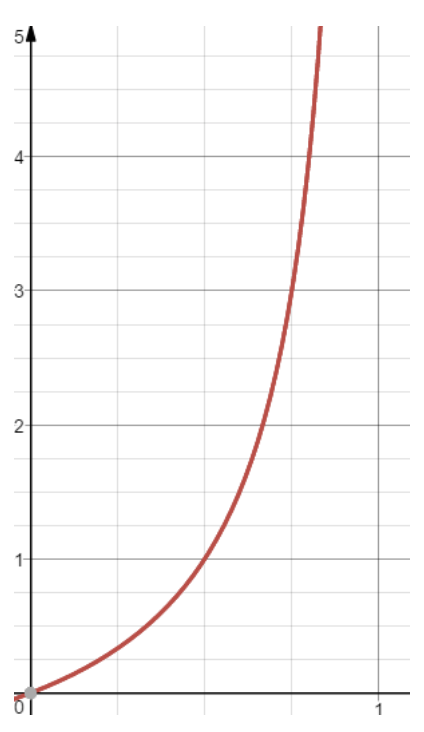
로지스틱 함수는 아래 그림과 같이 S-curve 함수를 나타낸다. 실제로 많은 자연, 사회현상에서는 특정 변수에 대한 확률 값이 선형이 아닌, S-curve 형태를 따르는 경우가 많다. 𝒙값으로 어떤 값이든 받을 수 있지만, 출력 결과(𝒚)는 항상 0에서 1 사이의 값이 된다. Cumulative distribution function(누적 분포 함수) 요건을 충족한다고 볼 수 있다.
시그모이드 함수라고 명명하기도 한다.
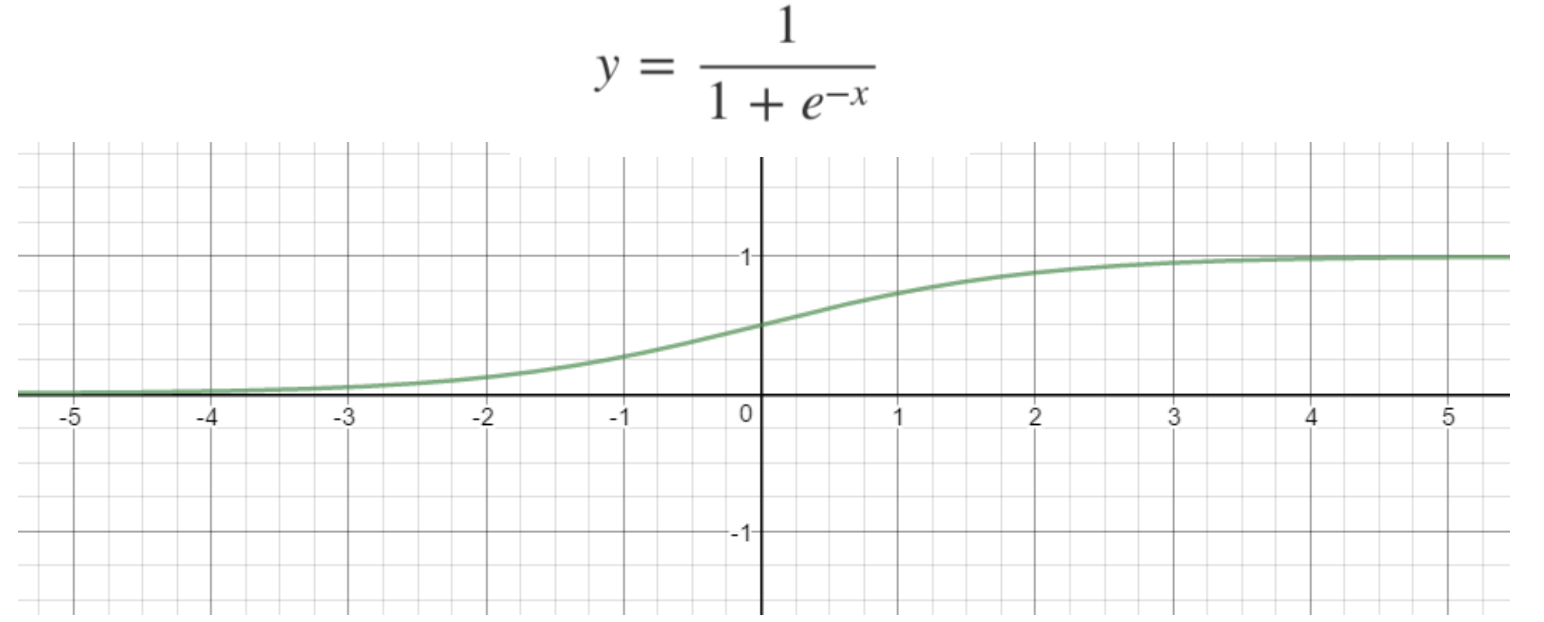
-
Odds
승산이란, 임의의 사건 A가 발생하지 않을 확률 대비 일어날 확률의 비율이다.
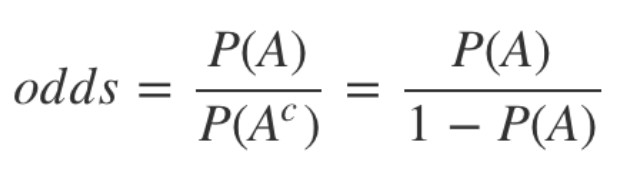
P(A)가 1에 가까울수록 승산은 커지고, 반대로 P(A)가 0이라면 승산은 0이다.
-
이항 로지스틱 회귀
𝑌가 범주형일 경우, 회귀 모델을 적용할 수 없다.
-
𝑌를 확률식으로 바꿔보면 (좌변 [0, 1], 우변 [-∞, ∞])
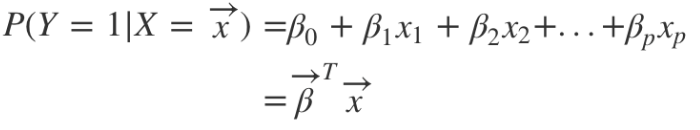
-
𝑌를 승산으로 바꿔보면 (좌변 [0, ∞], 우변 [-∞, ∞])
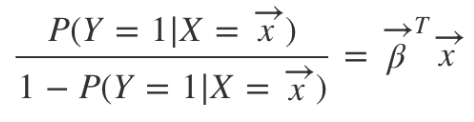
-
𝑌 승산에 ㏒를 취하면 (좌변 [-∞, ∞], 우변 [-∞, ∞])
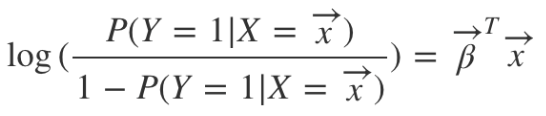
-
𝒙가 주어졌을 때 범주 1일 확률을 p(𝒙), 위 식 우변을 a로 치환해 정리하면
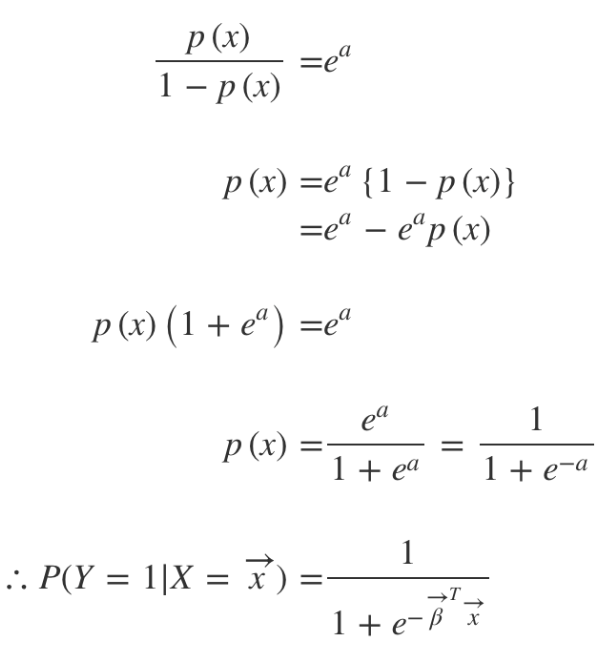
-
-
Decision boundary 이항 로지스틱 회귀의 결정 경계
범주 정보를 모르는 입력 벡터 𝒙를 넣으면 범주 1에 속할 확률을 반환하며, 범주 1로 분류하는 판단 기준은 아래와 같다.
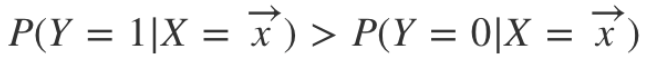
-
범주가 두 개 뿐이므로, 위 식 좌변을 p(𝒙)로 치환하면
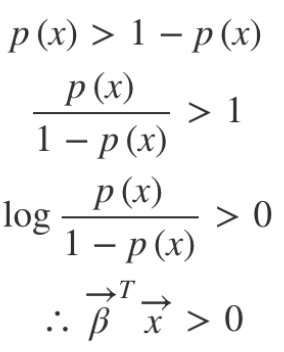
마찬가지로 βᵀ𝒙 < 0 이면 데이터 범주를 0으로 분류하게 되며, decision boundary는 βᵀ𝒙 = 0인 hyperplane이다.

-
-
다항 로지스틱 회귀
-
이항 로지스틱 회귀 모델을 통한 다항 로지스틱 회귀 문제 풀기
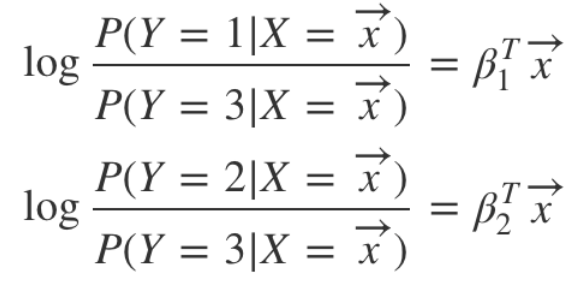
-
세 번째 범주에 속할 확률 = 1 - (첫 번째 범주에 속할 확률) - (두 번째 범주에 속할 확률)
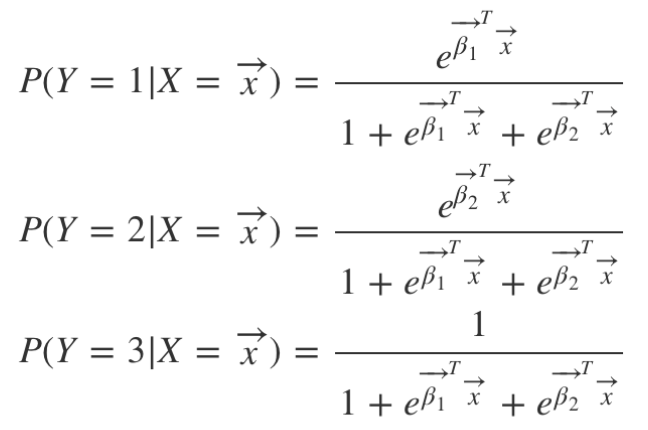
-
K개 범주를 분류하는 다항 로지스틱 회귀 모델의 입력 벡터 𝒙가 각 class로 분류될 확률
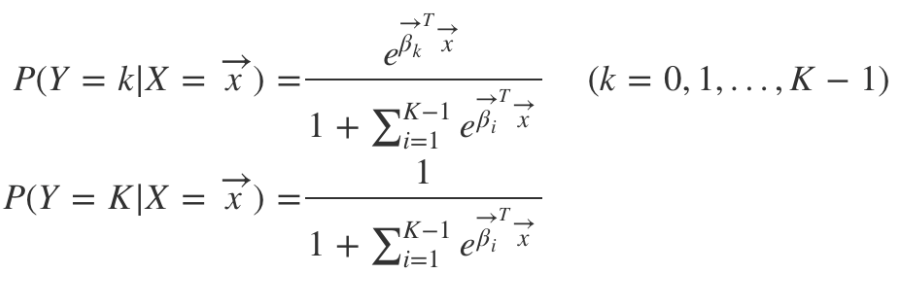
-
-
다항 로지스틱 회귀와 소프트맥스
-
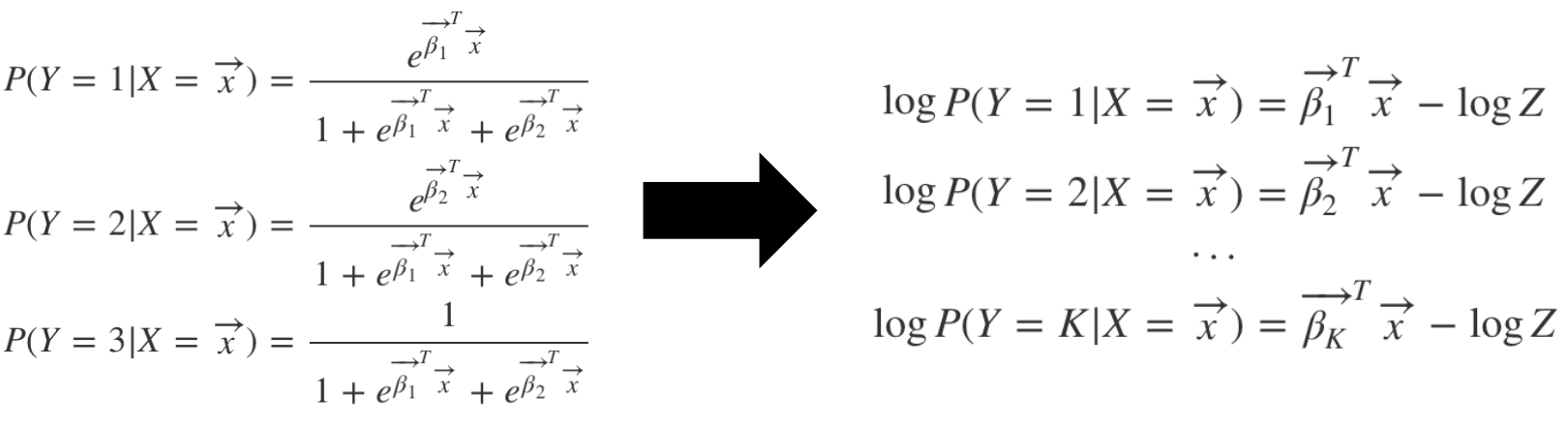
‘로그승산’으로 된 좌변을 ‘로그확률’로 변경
-
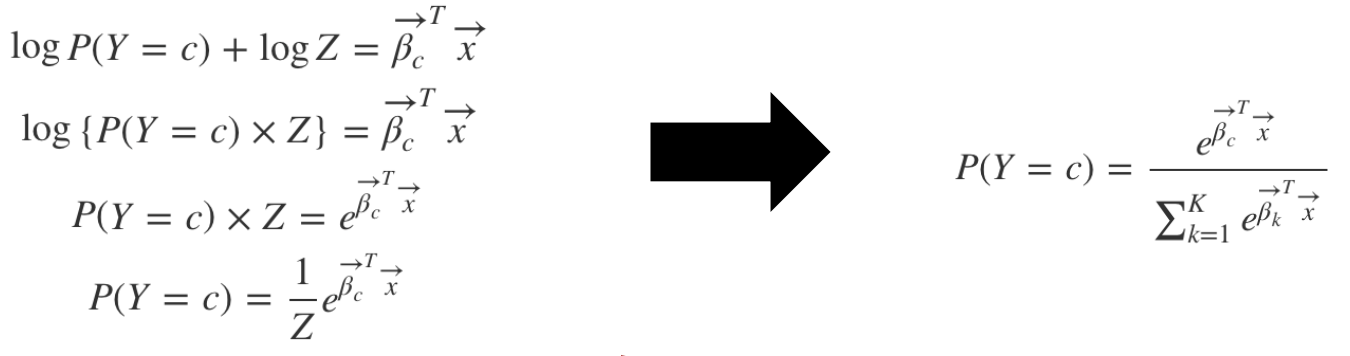
로그 성질을 활용해 𝒄번째 범주에 속할 확률을 기준으로 식을 정리
-
전체 확률 합은 1
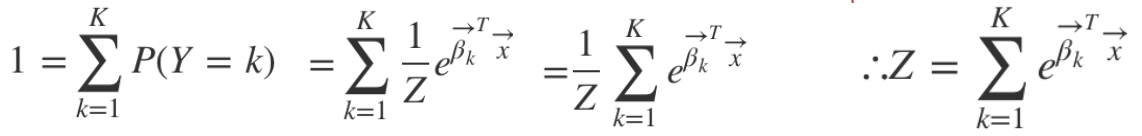
-
오랜만에 보는 수식들에 머리가 지끈거리긴 하다. 하지만 다양한 방법론들을 단순히 library에서 꺼내 쓰는 것이 아닌, 원리를 이해하고 사용할 수 있어야 적재적소에서 꼭 필요한 방법론들을 자유자재로 활용할 수 있을 것이다.